N극 또는 S극만을 가진 자석(자기단극자)을 일반 자석과 백금을 조합한 간단한 구조로 만들 수 있다는 것을 이론적으로 설명했다는 보도가 나왔습니다. 도쿄도립대학원 이공학연구과 多々良源 준교수와 竹内祥人 연구원이 실시한 연구입니다.
(PDF 파일) N極・S極だけをもつ磁石・磁気モノポールの発見
http://www.tmu.ac.jp/news/topics/4376.html?d=assets/files/download/thesis/press_120227.pdf
자료에 따르면, 모노폴(monopole)을 자석과 백금의 접합이라는 간단한 구조로 만들 수 있다면, 정보기기 내에서 N극만을 갖는 자석을 만드는 것이 가능하게 되어, 자원매장량에 문제가 있는 희토류 금속을 이용하지 않고도 고밀도의 장치를 만들 가능성이 있다는 것. 또한 모노폴을 조작하고 흐름을 만들면 자기장과 전기장을 대등하게 조작할 수 있게 되어 지금까지의 동작원리를 넘어선 새로운 정보전달과 정보기록이 가능하게 될 것으로 기대된다고 합니다.
자석(상층)과 백금(하층)의 접합구조에서 발생하는 자기단극자류와 모노폴이 만드는 전류
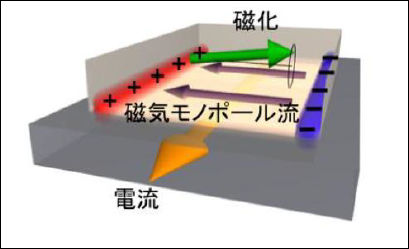
상대론적 효과(스핀궤도 상호작용)과 자석내의 자화운동에서 생성되는 자기단극자(스핀덤핑 모노폴)의 개념도

Wikipedia에서 '자기단극자'에 대해 알아보면, 자석은 N극, S극의 두 극이 항상 존재하며 이 조합을 자기쌍극자라고 합니다. 하나의 극만을 가진 자석, 즉 자기단극자(모노폴)는 현재까지 관측되지 않았고 존재하지 않는 것으로 간주합니다. 예를 들면 끝이 각각 N극과 S극으로 되어있는 막대자석을 중간에서 둘로 접는다 해도 마찬가지로 끝이 각각 N극과 S극으로 되어있는 막대자석이 되며 N극과 S극만을 추출할 수 없습니다.
전자석을 생각하면 이것을 쉽게 이해할 수 있습니다. 전자석은 전류를 흘린 코일이며, 이것을 둘로 나누어도 감긴 수가 절반인 전자석이 두 개가 만들어집니다. 영구자석에 대해서도 그것을 구성하는 물질의 원자가 전자석과 같은 역할을 하고있는 것이며 원리는 동일합니다. 맥스웰의 방정식으로 대표되는 고전전자기학은 이 전제하에 구성되어 있습니다.

한편, 전기는 플러스와 마이너스가 존재하고 이것들은 단독으로 추출할 수 있습니다. 이것은 전기의 근원이 플러스인 양성자와 마이너스인 전자에서 유래하고 있기 때문입니다. 그리고 고전전자기학은 전기와 자기의 관계에 대해 대칭이며, 이 관계를 반대로 하는 것이 가능합니다. 코일에 흐르는 전기에 의해 자력이 발생하는 즉 원주 위를 회전하는 전자의 운동에 의해 자기장이 생깁니다. 이것을 자기단극자가 원주 위를 회전하는 것에 의해 전계가 생긴다는 모델로 대체할 수 있습니다. 즉, 맥스웰의 방정식은 자기단극자의 존재를 허용하도록 쉽게 변경할 수 있습니다. 또한 1931년 폴 디랙은 양자역학에서 자기단극자를 고려할 수 있고 게다가 그것이 가능하기 위한 조건에서 전하의 최소단위가 도출되는 것으로 나타나 자기단극자가 일약 주목을 받았습니다.
"전자처럼 전기의 근원이 되는 전하를 가지고 자유롭게 움직이는 입자가 존재하니, 자기의 근원인 자하를 가진 입자도 존재한다고 생각하는 것은 지극히 당연하다."
여기에는 근본적인 문제가 있는데, '중력 이외의 자연계에 존재하는 근원적인 힘을 통일하는 대통일 이론에서 자기단극자의 생성은 우주 탄생의 초기에 해당하는 거대한 에너지가 필요한 것으로 나타났는데, 당연히 현재 지구상에서 그것을 만들어 낼 방법은 없다는 것.

그러나 이번 발견은 '자석 내의 무거운 원소가 가지고 있는 상대론적 효과를 활용하여 실험실에서 자기단극자을 생성하는 것이 가능하다는 것을 밝힌 것으로, 물질 중의 자연법칙을 크게 발전시켰다'고 평가받고 있습니다.
전자기학이 완성된 19세기 이후 처음으로 우리는 전기와 자기를 대등하게 취급하는 것이 가능하게 되는 것입니다. 자기단극자를 활용한 이 기술은 기존의 방법으로는 가까운 미래에 한계를 맞는 장치의 고밀도 집적화 및 에너지 절약, 새로운 정보통신 기술의 개발 등에 활로를 개척할 가능성을 내포하고 있습니다.
이 성과는 일본물리학회가 발행하는 영문 잡지 Journal of the Physical Society of Japan(JPSJ)의 주목 논문(Editors 'Choice)으로 게재될 예정이라고 합니다.
'과학 & 기술' 카테고리의 다른 글
| 원자가 결합하여 분자가 되는 과정을 동영상으로 촬영하는 데 성공 (0) | 2021.01.23 |
|---|---|
| 유네스코가 지정한 '빛과 광학기술의 국제년 '국제광년' (0) | 2021.01.23 |
| 삼상교류(three-phase current)에 대한 이해 (0) | 2021.01.22 |
| '용량 무한대의 HDD'가 실현될 새로운 물리현상을 발견 (0) | 2021.01.22 |
| 자성이란 무엇인가...전자운동에 의한 자기발생 (0) | 2021.01.22 |
| 테슬라가 배터리의 제조과정을 동영상으로 공개 (0) | 2021.01.21 |
| 분전반의 퓨즈를 확인하는 방법 (0) | 2021.01.21 |
| 주요 전자부품의 기능 간략정리 (0) | 2021.01.21 |



