
수학의 양수(positive number)는 0보다 큰 실수를 말한다. 대조적으로 음수(negative number)는 0보다 작은 실수이다.
수학에서 음수는 마이너스 기호를 숫자 앞에 붙여 표현하지만, 부기 등에서는 숫자를 붉게 하거나 삼각형을 숫자 앞에 붙여서 나타낼 수도 있다.
제로는 증감이 없는 상태이기 때문에 양도 음도 아니다. 음수가 아닌 수(non-negative number)는 제로보다 작지 않은, 즉 제로 또는 양의 실수이다. 양이 아닌 숫자(non-positive number)는 제로보다 크지 않은, 즉 제로 또는 음의 실수이다.
복소수의 체계로 생각하고 있다면, 그 중 실수에 대해서만 양음을 논하고 허수는 양도 음도 없다고 한다. 예를 들어 '양수'라고 말하면, 그것은 실수임을 암시적으로 나타내는 것이지만, 명확히 하기 위해 '양의 실수'라고 표현할 수도 있다.

음수
음의 정수는 방정식 x - y = z가 어떤 x와 y에 대해서도 z에 관한 방정식으로 의미를 갖도록 자연수 체계를 확장하여 얻어지는 것이라고 생각된다. 이러한 음의 정수를 파악하는 방법과 동일한 방법으로 음의 유리수와 음의 실수도 얻을 수 있다.
음수는 온도와 같이 측정에서 제로보다 낮은 값을 설명하는 데 유용하다. 부기에서도 부채의 표현에 사용할 수 있다. 부기에서 부채는 종종 붉은 숫자(적자)와 삼각형을 앞에 붙인 숫자로 나타낸다.
음수가 아닌 수
제로에 동일하거나 그것보다 큰(즉 양이거나 제로이다) 실수를 음수가 아닌 실수라 한다.
덧셈과 뺄셈
수열은 영 · 양수 · 음수의 세 가지 조합으로 구성되어 있으며 기준점이 제로, 기준점으로부터 증가하고 있는 분이 양수, 기준점으로부터 줄어들고 있는 분이 음수가 된다.
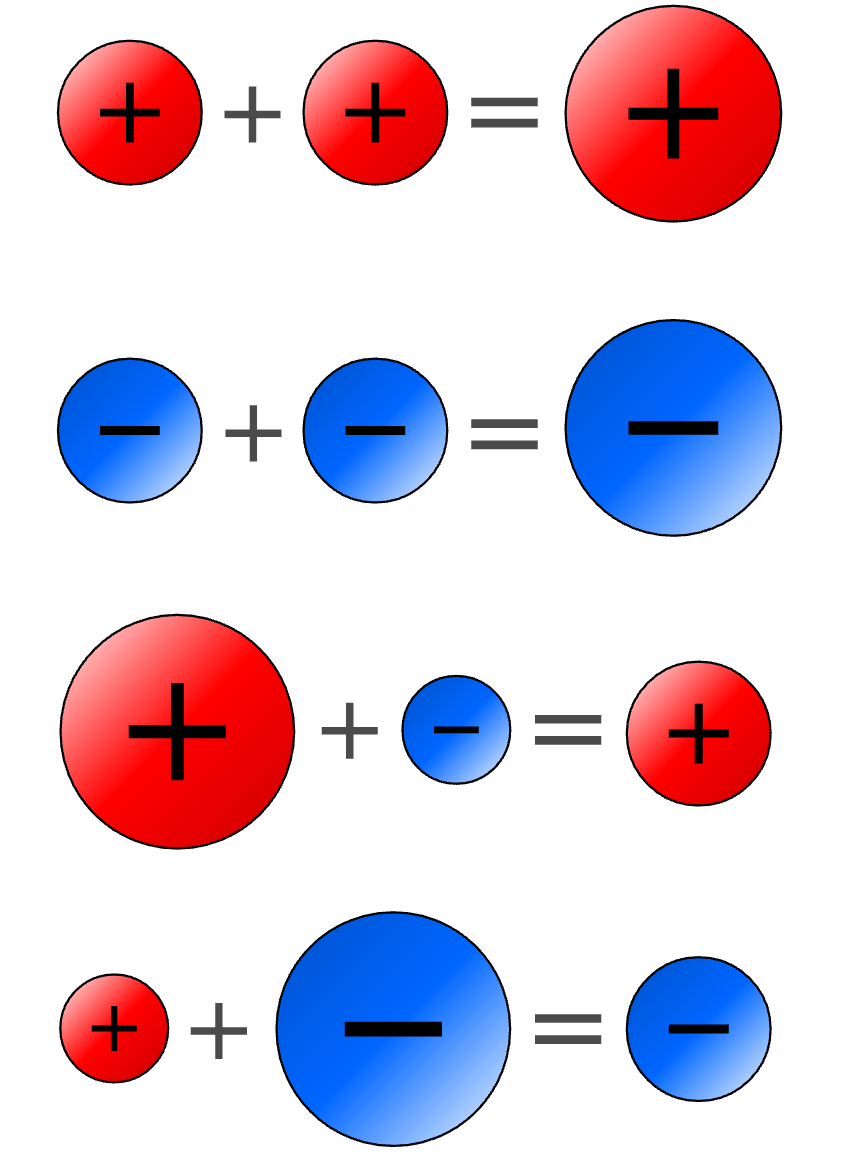
따라서 가산 및 감산에서는 음수는 부채이며, 양수는 수익이라고 생각할 수 있다. 마찬가지로 시간과 세대의 거리로 계산하면 제로는 현재와 나 자신, 음수는 과거와 연장자(부모나 조부모 등), 양수는 미래와 연하자(자녀와 손자 등)인 것으로 생각할 수도 있다.
음수를 추가하는 것은 해당 양수를 줄이는 것이다. 반대로 음수를 줄이는 것은 해당 양수를 더하는 것이 된다.
감산과 음수 부호의 개념혼동을 피하기 위해 음수 부호를 위첨자로 쓰는 경우도 있다(회계는 음의 부호를 △로 표현한다).
5 + (-3) = 5 - 3 = 2
(5원을 가지고 3원을 빌리면, 순자산은 2원)
4 - 6 = -2
(4원을 가지고 6원을 사용하면 부채 2원이 남는다)
5 - (-2) = 5 + 2 = 7
(순자산 5원을 가지고 빚을 2원 줄이면 새로운 순자산은 7원이 된다)
곱셈
음수를 곱은 양음의 방향을 반전시키게 된다. 음수와 양수를 곱하면 곱은 음수로 유지된다. 하지만 음수에 음수를 곱하면 곱은 양수가 된다.
(-20) × 3 = -60
(부채 20원을 3배로 늘리면 부채는 60원이 된다.)
(-40) × (-2) = 80
(뒤로 시간당 40km 진행하는 차량은 2시간 전에 현재 위치에서 앞쪽으로 80km 위치에 있었다.)
이것을 이해하는 방법의 하나로는, 양수에 의한 곱셈을 덧셈의 반복으로 간주하는 것이다. 3 × 2는 각 그룹이 2를 포함한 3개의 그룹으로 생각한다. 따라서 3 × 2 = 2 + 2 + 2 = 6이고 당연히 -2 × 3 = (-2) + (-2) + (-2) = -6이다.
음수에 의한 곱셈도 가산의 반복으로 볼 수 있다. 예를 들어 3 × -2는 각 그룹이 -2를 포함한 3개의 그룹으로 생각된다.
3 × -2 = (-2) + (-2) + (-2) = -6
이것은 곱셈의 교환법칙을 만족한다.
3 × -2 = -2 × 3 = -6
'음수에 의한 곱셈'과 같은 해석을 음수에 대해서도 적용하면 다음과 같다.
-4 × -3 = - (-4) - (-4) - (-4)
= 4 + 4 + 4
= 12
그러나 형식적인 관점에서 두 음수의 곱셈은 곱의 합에 대한 분배법칙에 의해 직접 얻을 수 있다.
-1 × -1 = (-1) × (-1) + (-2) + 2
= (-1) × (-1) + (-1) × 2 + 2
= (-1) × (-1 + 2) + 2
= (-1) × 1 + 2
= (-1) + 2
= 1

나누기
나누기도 곱셈과 마찬가지로 음수로 나누면 양음의 방향을 반전시키게 된다. 음수를 양수로 나누면 몫은 음수로 유지된다. 그러나 음수를 음수로 나누면 몫은 양수가 된다.
두 수의 부호가 다르다면 지수는 음수가 된다.
(-90) ÷ 3 = -30
(부채 90원을 3명으로 나누면 부채는 30원씩 상속된다.)
24 ÷ (-4) = -6
(동쪽을 양수 서쪽을 음수로 하는 경우 : 4시간 후에 동쪽으로 24km 지점에 이동하는 차량은 1시간 전에 서쪽으로 6km의 위치에 있었다.)
두 수가 같은 부호를 갖는다면 모두 양수가 된다.
(-12) ÷ (-3) = 4
거듭제곱
거듭제곱은 곱셈이나 나눗셈과 마찬가지로 지수가 양수라면 'n승'에 두배가 된다. 그러나 지수가 음수라면 '1/n승'으로 분할된다.
3^3 = 27
(× 3 × 3 × 3 = 27)
3^-3 = 1/27
(÷ 3 ÷ 3 ÷ 3 = 1/27)
360 × 2^3 = 2880
(360 × 2 × 2 × 2 = 2880)
36 × 5^-1 = 7.2
(36 ÷ 5 = 7.2)
출처 참조 번역
· 正の数と負の数
https://ja.m.wikipedia.org/wiki/%E6%AD%A3%E3%81%AE%E6%95%B0%E3%81%A8%E8%B2%A0%E3%81%AE%E6%95%B0
'과학 & 기술' 카테고리의 다른 글
| 왜 전자가 흐르는 방향과 전류가 흐르는 방향은 다른가? (0) | 2021.01.28 |
|---|---|
| 마이너스란 무엇인가? 마이너스의 세계는 정말 존재하는가 (0) | 2021.01.27 |
| 기적의 숫자 '142857'에 숨겨진 비밀 (0) | 2021.01.27 |
| 5분 안에 충전할 수 있는 전기자동차용 배터리의 비밀 (0) | 2021.01.27 |
| 인류 역사상 가장 빠른 물체는 '핵실험으로 날라간 맨홀 뚜껑' (0) | 2021.01.26 |
| 음수(陰數)의 기원 (0) | 2021.01.25 |
| 양수 · 음수 그리고 자연수와 정수에 대해서 (0) | 2021.01.25 |
| 세계 최초로 결정이 완성되는 순간의 촬영에 성공 (0) | 2021.01.25 |



