
미국수학회에서 두 명의 10대 소녀가 피타고라스의 정리에 대한 새로운 증명방법을 프레젠테이션한 것이 화제가 되고 있습니다. 응용수학 전문가인 키스 맥널티 씨는 “성별, 민족, 사회인구학적 배경에 관계없이 기쁨과 열정이 있으면 누구나 연구분야에서 우수성을 달성할 수 있음을 보여주는 놀라운 사건"이라고 평가했고 증명방법 자체도 파문을 부르고 있습니다.
Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem | by Keith McNulty | Apr, 2023 | Medium
https://keith-mcnulty.medium.com/heres-how-two-new-orleans-teenagers-found-a-new-proof-of-the-pythagorean-theorem-b4f6e7e9ea2d
Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem
An inspirational example of how elementary math is open to everyone
keith-mcnulty.medium.com
American Mathematical Society(미국수학회, AMS)에서 루이지애나주 뉴올리언스 출신의 10대 소녀인 칼시아 존슨 양과 네키야 잭슨 양이 프레젠테이션을 했고 피타고라스 정리의 새로운 증거를 보여주었습니다. 두 소녀는 학생이고 아프리카계 미국인 여성이라는 특징은 수학회의 대다수를 차지하는 인종과는 다른데 맥널티 씨는 “선택한 연구분야에서의 우수성은 누구나 항상 달성 가능하다는 것을 보여주는 훌륭한 사건"이라고 보았습니다.
또 맥널티 씨에 의하면 이 프레젠테이션이 큰 화제가 된 이유는 증명방법 자체가 고명한 수학자들을 놀라게 했다는 것.
원래 피타고라스의 정리란 '직각삼각형의 3변의 길이 중 2변을 알고 있으면 나머지 1변의 길이를 계산할 수 있다'는 것으로 'a^2 + b^2 = c^2'라는 수식으로 표현됩니다. 한국에서는 중학과정에서 학습하는 수식인데 수식의 증명에는 수백 가지의 다른 패턴이 나타납니다.
이 피타고라스의 정리의 증명에 삼각법을 이용한 것이 수학회에 큰 충격을 주었다고 맥널티 씨는 지적했습니다. 삼각법이란 삼각형의 모서리의 크기와 변의 길이의 관계를 기초로 다른 증명이나 측량 등의 연구에 응용하는 학문분야인데 그 삼각법 자체가 피타고라스의 정리에 의존하고 있기 때문에 삼각법으로 피타고라스의 정리를 증명하는 것은 '전제 속에 결론을 넣는다'는 이른바 순환론법에 해당하기 때문에 피타고라스의 정리를 삼각법으로 증명하는 것은 불가능이라고 생각되어 왔습니다.
그러나 맥널티 씨에 의하면 피타고라스의 정리는 삼각법으로 증명할 수 없다는 관점은 최근 수십 년에 의문시되는 케이스가 많아 증명이 몇 번이나 시도되어 왔다고 합니다. 그러므로 존슨 양과 잭슨 양의 증명이 '최초의 삼각법에 의한 피타고라스의 정리 증명'이라는 것은 아니지만, 맥널티 씨는 그녀의 증명을 "지금까지 본 가장 아름답고 가장 간단한 삼각법의 증명일 수 있다”고 높이 평가했습니다.
삼각법을 이용한 피타고라스의 정리의 새로운 증명에 대해 맥널티 씨는 아래의 그림으로 나타내었습니다. 그림에서는 a≠b라고 가정한 변 a, b, c를 가지는 직각삼각형에 대해서 변 b와 c 사이의 각도를 α, 변 a와 c 사이의 각도를 β로 했습니다. 이 직각삼각형에 대해서 우선 변 b를 축에 수평방향으로 반전한 카피를 형성하고, 변 c에 수직인 직선 A를 각 β로부터 연장한 후 직선 A와 변 c를 연결하는 직선 C를 그린다는 3단계를 수행합니다. 그러면 큰 직각삼각형이 형성되어 그 안에 원래의 직각삼각형과 유사한 직각삼각형을 왼쪽 위에서 점차 작아지는 형태로 무한하게 그릴 수 있습니다. 이 무한한 유사 삼각형 시퀀스를 사용하여 직선 A와 C의 길이를 도출하는 것이 존슨 양과 잭슨 양의 증명입니다.
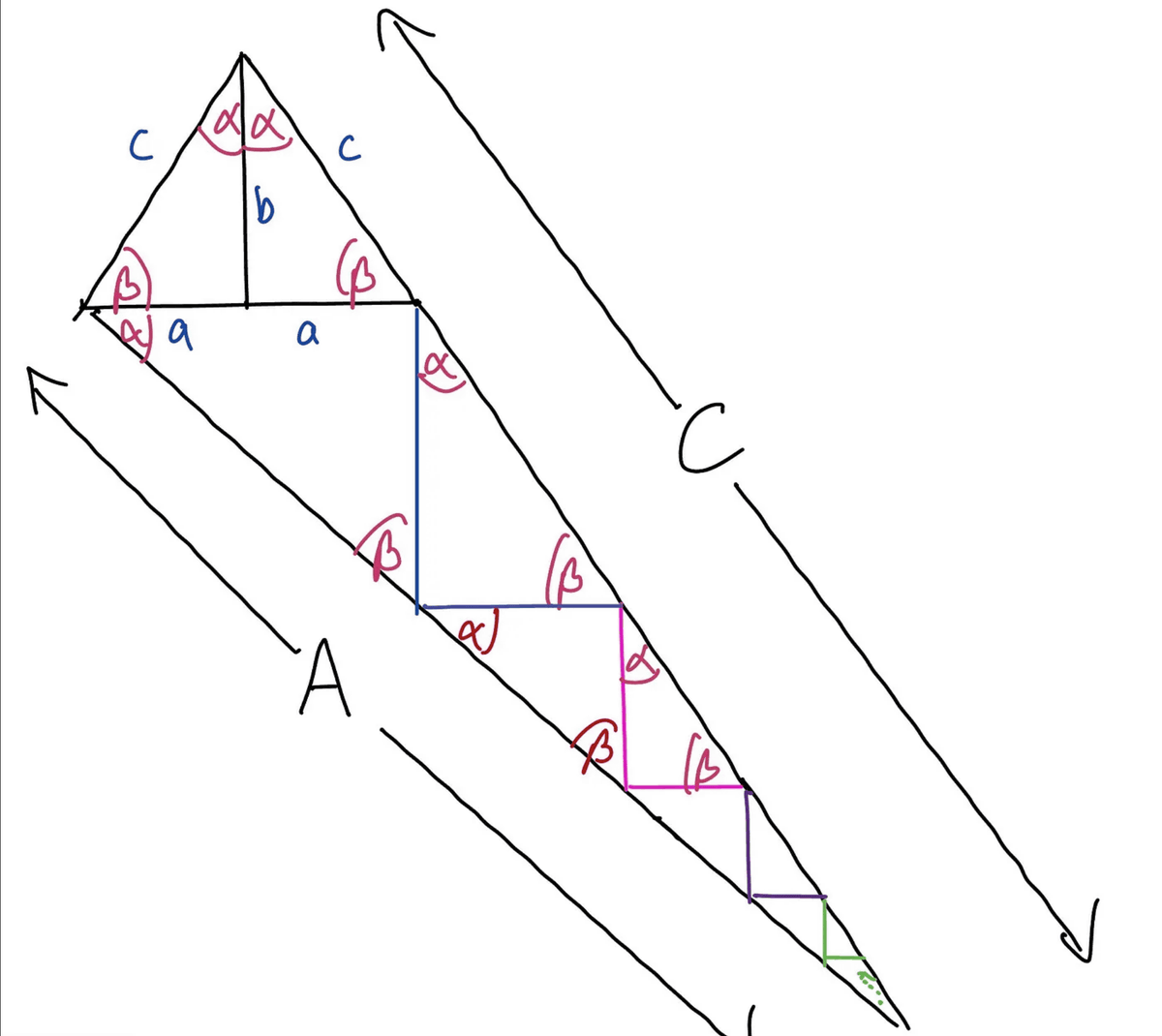
그림에서 알 수 있듯이 세 번째 삼각형의 한 변은 2a로 표현되며 'sinα = consβ = a/c'와 'cosα = sinβ = b/c'라는 삼각비를 사용하면 사변은 '2a/sinβ=2ac/b'라고 나타낼 수 있습니다. 이와 같이 무한에 이어지는 유사 삼각형의 경우 인접한 삼각형의 변으로부터 삼각비를 사용해 표현할 수가 있습니다. 이 때 유사 삼각형 전체의 변 A의 길이는 초항 (2ac)/b, 공비 'a^2/b^2의 등비급수의 합이 되어 아래와 같이 나타낼 수 있습니다.

또한 직선 C도 마찬가지로 초항 (2a^2c)/b^2와 공비 a^2/b^2를 가지는 등비급수이며 아래와 같이 나타납니다.
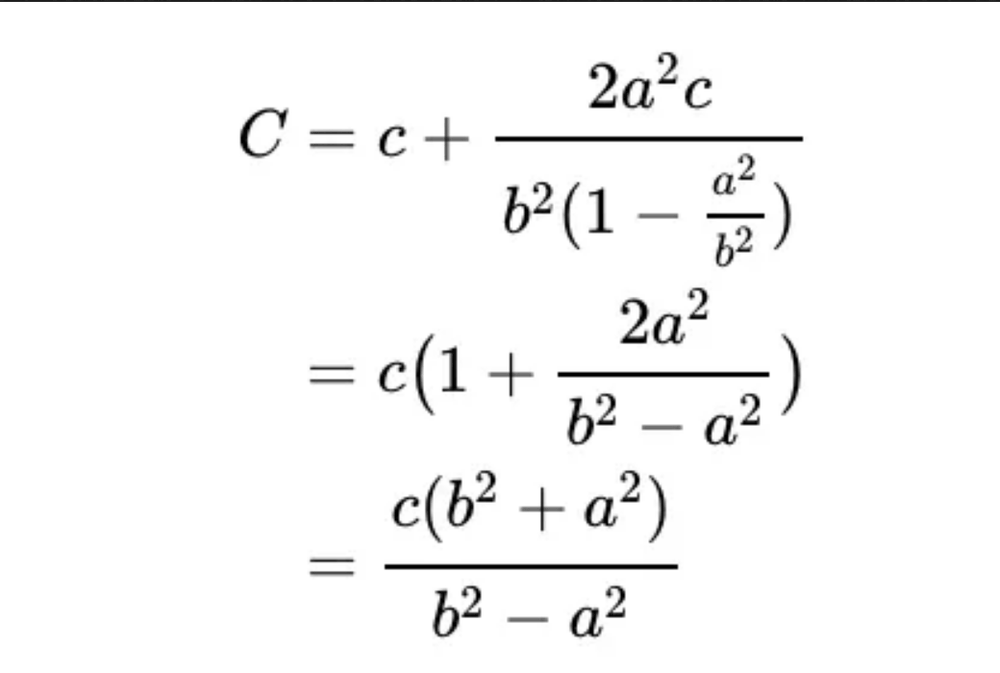
여기에 표시된 A와 C의 비율을 계산하면 다음과 같이 되고 삼각함수에서는 'sinθ=θ의 대변/사변'으로 나타내므로 직선 A/C=sin(2α)라는 것을 알 수 있습니다.

게다가 위 그림의 제일 먼저 직각삼각형을 수평방향으로 카피한 것으로 2개의 직각삼각형을 맞춘 하나의 삼각형은 이등변 삼각형이 됩니다. 여기서 증명에 삼평방의 정리를 사용하지 않는 정현정리를 이용해 직선 A와 C의 비에 관한 식을 변환하면 최종적으로 아래와 같은 식이 됩니다. a, b, c가 모두 0이 아니기 때문에 분자가 동일하면 분모가 동일해야 합니다. 따라서 'a^2+b^2 = c^2 '가 나옵니다.

Hacker News에서도 이 증명에 대해 화제가 되고 있는데 "이 증명은 삼각형의 변의 비율로서 사인이나 코사인이 존재한다고 가정하고 있는 것만이고 삼각법을 사용한다는 문구는 오해를 초래하는 표현이라고 지적하는 의견이 있는 한편, 종래는 사인의 법칙을 증명에 사용할 수 없다는 신념이 있었고 그 때문에 피타고라스의 정리를 삼각법, 또는 사인이나 코사인을 이용해 증명하는 것은 불가능하다고 생각되었는데 이것이 타파되었기 때문에 창조적이고 예상치 못한 증명이라고 불렸다고 생각된다.”고 존슨 양과 잭슨 양의 증명의 무엇이 획기적이었는지를 설명하는 댓글도 달렸습니다.
'과학 & 기술' 카테고리의 다른 글
| 의류건조기 안에서 방사선량이 높아지는 이유 (0) | 2023.05.21 |
|---|---|
| 반물질을 뇌운 속에서 발견? (0) | 2023.05.18 |
| 반양성자의 질량을 10자리수 측정에 성공 (0) | 2023.05.09 |
| 왜 소수는 나선을 그리는가 (0) | 2023.05.09 |
| MRI의 해상도를 기존보다 6400만 배 향상시키는 기술이 등장 (0) | 2023.04.21 |
| 최신 방범기능을 가진 '도요타 RAV4'이 도난피해를 입다 (0) | 2023.04.07 |
| 소립자 'W보손'의 질량이 지금까지의 추측을 웃돌 가능성 (0) | 2023.03.25 |
| 미래가 과거에 영향을 미친다는 '역행성'에 주목 (0) | 2023.03.21 |



