
멀리 보는 것은 과거를 보는 것으로, 지구를 중심으로 '어디까지 보이는가?'라는 질문은 '얼마나 옛날이 보이는가?'와 같은 것입니다. 전자가 원자핵에 사로잡혀 우주가 맑아졌고 광자가 자유로워진 시대가 '보이는 한계'입니다.
빛 이외의 것을 통해서라도 우리와 어떠한 관계가 있을 수 있는 거리는 '지평선'까지가 한계입니다. 우주의 오랜 역사 속에서 우주가 맑아지기까지의 시간은 우주의 연령에 비하면 훨씬 짧기 때문에 지평선까지가 보이는 한계라고 생각해도 지장이 없을 것입니다.
그래서 지금까지의 이론이나 관측 사실을 의지해 상상할 수밖에 없습니다. 공간은 3차원이지만 상상하거나 그림에 그리기가 어렵기 때문에 2차원의 공간으로 상상해 봅니다. 지구에서 본 지평선까지의 공간이 완전히 우주에 포함되어 있으면 관측과 모순되지 않는다고 생각될지도 모릅니다. 우주를 직사각형으로 표현하고 유한의 크기(2차원이므로 넓이)의 도형이면 상관없습니다. 우리는 우연히 지금과 같은 위치에 있고 우주의 끝을 볼 수는 없지만 다른 곳에서는 우주의 끝의 영향이 나타난다고 생각할 수도 있습니다. 그런데 이러한 사고방식은 빅뱅 이론의 대전제였던 우주의 균일·등방성과 충돌합니다. 즉, 우리가 있는 장소는 특별한 장소가 아니고 우리가 관측하는 것은 다른 어느 장소에서도 관측할 수 있다는 것이 균일성이었습니다. 또 어느 방향을 봐도 같게 보인다는 등방성이 성립한다면 서쪽만 우주의 끝의 영향이 보이고 동쪽은 보이지 않는다고 말할 수 없습니다. 이 2개의 대전제가 성립한다면 우주는 무한히 넓거나 유한의 넓이의 경우에는 구의 표면과 같이 되어 있어야 합니다. 균일·등방성을 만족하는 무한히 넓은 면은 평면과 쌍곡면이 있습니다.
우주가 시작되었을 때 무한대의 공간에서 시작되었다는 것은 기이한 느낌이 들지만 시작의 순간을 모르기 때문에 이러한 가능성도 부정할 수 없습니다.
균일·등방성을 버린다면 빅뱅이론으로 설명할 수 있었던 여러 가지 관측 사실을 재차 검토할 필요가 생깁니다. 게다가 우리가 '특별한 장소'에 있다는 것을 설명해야 합니다.
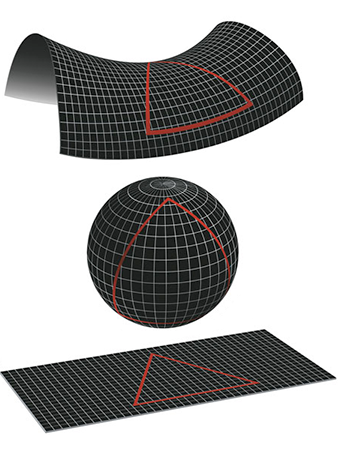
우주의 형태는 균일·등방성을 채우기 위해서는 구면, 평면, 쌍곡면 중 어떤 형태를 하고 있을 것입니다. 다만 이것은 공간이 2차원인 경우의 이야기로, 현실의 3차원의 경우에도 각각에 대응한 도형(수학 용어에서는 다양체)이 있습니다. 이 3가지의 도형을 기하학적 '곡률'로 구별할 수 있습니다. 구면은 양(플러스)의 곡률, 평면은 0, 쌍곡면은 음(마이너스)의 곡률을 가진다고 합니다. 구면의 경우 구의 반경의 제곱의 역수가 곡률입니다.
우주의 에너지 밀도와 우주의 형태에는 다음과 같은 관계가 있습니다.

현재의 우주의 밀도는 거의 임계 밀도와 같기 때문에 이 3가지 중 어느 것인지는 단정할 수 없지만 닫힌 우주(구면)에서도 열린 우주(쌍곡면)에서도 곡률이 거의 0에 가까운 경우에 있을 것입니다. 예를 들어 구면(닫힌 우주)에서 곡률이 크면 망원경으로 멀리 보면 자신의 뒤통수가 보인다거나 우주선으로 직진하면 원래 장소로 되돌아오는 현상이 발생합니다. 다만 반경이 충분히 커 현재의 지평선보다 훨씬 크면 이런 일은 일어나지 않습니다.
결국 우주의 에너지 밀도를 정확히 모르기 때문에 거의 평탄하지만 어떤 형태가 되어 있는지는 단정할 수 없습니다.
출처 참조 번역
- Wikipedia
- 宇宙の大きさ、宇宙の形
https://astr.phys.saga-u.ac.jp/~funakubo/BAU/chapter6/chapter6-5.html
'우주 & 천문학' 카테고리의 다른 글
| 은하단의 원소 조성은 균일 (0) | 2024.02.19 |
|---|---|
| 우주에서의 분자의 신비 (0) | 2024.02.06 |
| 우주의 형태(shape of Universe) (0) | 2024.02.02 |
| NASA, 제임스웹 우주망원경이 포착한 19개의 은하 사진을 공개...적외선 관측으로 드러난 나선은하의 구조 (0) | 2024.02.01 |
| 달이 냉각수축하면서 발생하는 '월진'이 아르테미스 계획이나 월면 콜로니 건설에 악영향을 미칠 가능성 (0) | 2024.01.31 |
| 우주의 형상은 도넛형? (0) | 2024.01.31 |
| 우주의 형태(곡률) (0) | 2024.01.30 |
| 최근 발견된 초거대 구조 '라니아케아 초은하단'이란 무엇인가 (0) | 2024.01.28 |



