
우주의 모양은 일반적으로 '곡률'로 결정됩니다. 2차원의 평면에서 그것이 구의 표면인지 아니면 평면이 영원히 계속되는지는 3차원의 세계로부터 부감적으로 보지 않으면 그 전모를 이해할 수 없습니다.
그와 마찬가지로 우리가 사는 3차원 우주의 공간적인 전모를 이해하기 위해서는 더 높은 차원에서의 시점이 필요하기 때문에 3차원의 공간 안에 사는 3차원의 몸을 가진 우리는 감각적으로 우주의 전모를 상상하기가 어렵습니다. 그래서 상상하기 쉽도록 일단 2차원으로 차원을 떨어뜨려 생각합니다. 2차원 세계의 모양은 곡률에 따라 3가지 패턴일 수 있습니다.
먼저 곡률이 0이면 완전히 평평한 평면입니다. 곡률이 플러스인 경우 어느 방향으로도 동일하게 구부러져 있는 상태로 구면과 같이 닫힌 2차원 세계가 됩니다. 곡률이 마이너스인 경우 시트의 방향에 따라 구부러지는 방향이 달라 말의 안장 모양의 세계가 됩니다.
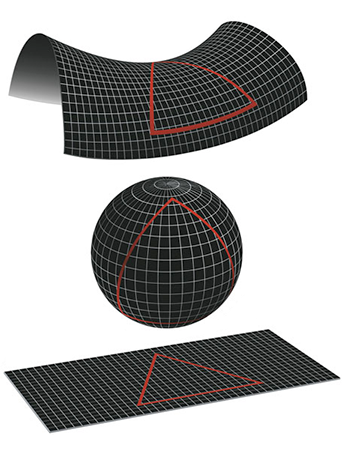
이러한 2차원 세계에 사는 2차원 주민들에게 이 세계의 모양을 아는 방법이 있습니다. 그것은 이 평면 세계에 거대한 삼각형을 그려 내각의 합을 조사하는 방법입니다. 실은 곡률에 따라 내각의 합이 다릅니다. 평평한 평면의 경우 삼각형의 내부 각도의 합은 180도입니다. 곡률이 플러스인 평면에서 삼각형의 내부 각도의 합은 180도보다 커집니다. 곡률이 마이너스인 평면에서 삼각형의 내부 각도의 합은 180도보다 작습니다.
이 특성은 우리가 사는 3차원 공간에서도 마찬가지입니다. 2차원 세계와 마찬가지로 공간 내에서 거대한 삼각형을 묶어 내각의 성질을 조사하는 식으로 이 우주공간의 곡률과 우주의 형상을 간접적으로 알 수 있습니다. 과학자들은 탄생으로부터 1억 년 후의 우주의 크기를 저변, 현재의 지구를 하나의 정점으로서 삼각형을 설정해 실제로 그 기하학적 성질을 조사했습니다.
1억 살의 우주에 대한 정보는 우주배경복사로부터 얻을 수 있습니다. 우주배경복사는 우주 탄생으로부터 약 38만 년 후 우주공간에 채워진 최초의 빛으로, 지금의 지구에도 우주의 모든 방향으로부터 거의 균등하게 도달하고 있습니다.
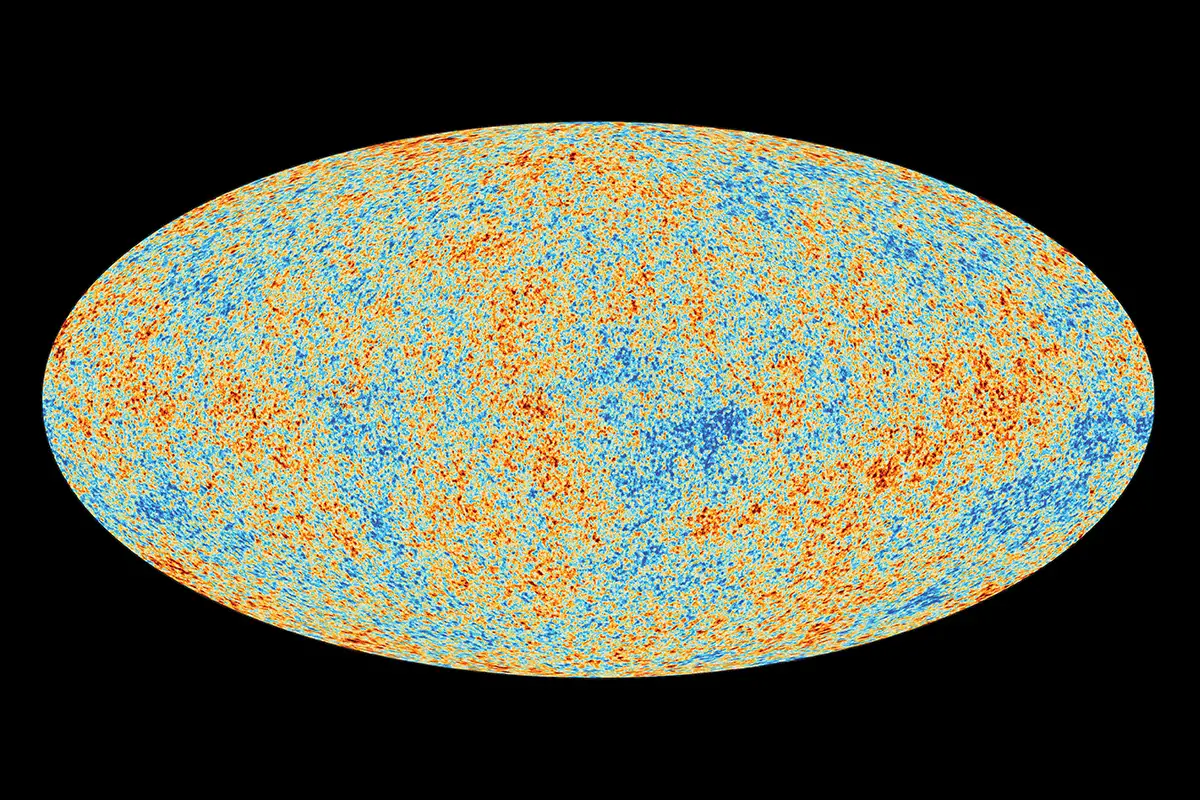
우주배경복사를 이용한 관측의 결과, 거대한 삼각형은 이 우주가 평평한 우주임을 나타내었습니다. 이에 현재 이 우주는 평평한 우주일 가능성이 높다고 생각되고 있습니다.
▣ 평탄한 도넛형
곡률이 0인 우주는 평평한 우주, +인 우주는 닫힌 우주, -인 우주는 열린 우주라고 불립니다. 닫힌 우주에서는 체적이 유한하지만 특정 방향으로 계속 진행하면 같은 장소로 돌아올 수 있을 것입니다. 또 다른 우주에서는 가장자리라는 것이 없는 한 특정의 방향으로 어디까지나 계속 진행할 수 있어서 체적은 무한하게 퍼져 있을지도 모릅니다. 우주가 평탄하면 그 공간에는 끝이 없을 것입니다.
하지만 실은 평탄한 우주에서도 크기가 유한한 경우가 있습니다. 공간이 2차원인 경우로 생각하면, 먼저 평면에 직사각형(또는 정사각형)을 그립니다. 그리고 그 직사각형의 마주 보는 변을 같은 것으로 간주합니다.
위쪽과 아래쪽은 연결되어 있고 오른쪽과 왼쪽 가장자리도 연결되어 있습니다. 직사각형은 신축·변형이 자유자재인 고무 시트와 같은 것으로 되어 있다고 가정하고 먼저 직사각형의 좌우 모서리를 붙입니다. 그렇게 완성되는 것은 원통의 측면입니다. 이 원통을 꽉 구부려 늘려 상하의 변을 붙입니다. 그러면 도넛 모양이 됩니다. 이러한 형태를 수학적으로는 '토러스'라고 합니다.

불행히도 3차원 공간에서는 모든 점에서 곡률이 0인 평탄한 토러스를 만들 수 없습니다. 외측에서는 어느 방향을 봐도 똑같이 구부러져 있기 때문에 플러스 곡률, 안쪽에서는 방향마다 구부러진 방향이 다르기 때문에 마이너스 곡률이 되어 버립니다. 평탄한 토러스는 4차원 이상의 공간 안에서 밖에 실현할 수 없습니다.
이 우주가 같은 평탄한 우주라도 끝없이 공간이 퍼져 나가는 우주는 아니고, 그 형태의 후보의 하나로서 3차원의 평탄 토러스형의 우주가 존재한다는 것입니다.
▣ 평탄한 토러스 세계의 특징
2차원의 평탄 토러스 안에서의 물체의 움직임을 생각해 봅시다. 평면에 있는 토러스의 실체는 직사각형이었습니다. 그러나 위쪽과 아래쪽 가장자리는 연결되어 있고 오른쪽과 왼쪽 가장자리도 연결되어 있는 상태의 직사각형이었습니다. 이 직사각형 안에 2차원 사람이 있다고 가정하면 중간에서 왼쪽 끝까지 가서 한층 더 진행하면 오른쪽 끝에서 나오게 됩니다. 위쪽 끝까지 가서 더 나아가면 아래쪽 끝에서 나타납니다. 아케이드 게임이나 RPG의 세계는 이런 식인 경우가 자주 있습니다. 실은 많은 게임에서는 토러스 모양의 세계로 되어 있었던 것입니다.
실제 우주와 같은 3차원의 평탄한 토러스는 구체적인 형태를 상상하기는 어렵지만, 그 안에서의 물체나 빛의 움직임을 생각할 수 있습니다. 예를 들어 천장이나 바닥을 포함하여 인접한 6개의 면 모두가 다른 방에 연결되어 있는 직육면체의 방이 있었다고 합시다. 어느 방향이라도 좋기 때문에 방을 나오면 거기는 원래의 방과 완전히 같은 방입니다. 옆방을 보면 자신의 뒷모습이 무한하게 이어져 보입니다. 좌우의 방도 상하의 방도 전후의 방도 모두 지금 있는 방과 같고 어느 방에도 자신이 있는 것입니다. 이와 같이 같은 구조가 루프하고 있는 것이 3차원의 평탄 토러스의 세계입니다.
▣ 우주가 평탄한 토러스형인 증거
우주가 토러스처럼 연결되어 있는지 이해하는 열쇠는 우주배경복사에 있습니다. 초기 우주에서는 물질 밀도의 요동이 파동으로 존재했습니다. 이것은 음파와 매우 유사한 성질을 가지고 있습니다. 음파도 공기 밀도의 파동이기 때문입니다.

현을 비롯한 음파의 파장(소리의 높이)은 현의 길이에 의해 결정됩니다. 마찬가지로 우주의 물질 밀도의 요동의 파장은 우주의 크기에 의해 제한됩니다. 우주보다 큰 파장의 요동은 존재할 수 없습니다. 이 우주의 밀도 요동 정보는 우주배경복사에서 읽을 수 있습니다. 밀도 요동의 파장에 상한이 있으면 우주가 유한하다는 증거가 됩니다.
한층 더 컴퓨터 시뮬레이션으로 다양한 우주의 형태를 상정해 시뮬레이션 결과와 실제의 관측을 대조하여 이 우주가 도넛처럼 구멍이 뚫린 구조인지 아닌지까지 알 수 있다고 합니다. 연구팀은 컴퓨터 시뮬레이션 결과와 우주배경복사 데이터를 비교하여 우주의 크기와 형상을 구하고 그 결과를 2021년 7월에 발표했습니다. 연구 결과 우주의 크기는 관측 가능한 우주의 한계(약 450억 광년)의 약 3~4배 정도이며 도넛처럼 구멍이 뚫린 구조일 가능성이 보였습니다.
앞으로도 우주의 형태에 관한 연구가 진행되어 가고 있으며 새로운 발견이 기대됩니다.
출처 참조 번역
- Wikipedia
- 最新の観測で宇宙は「3次元のドーナツ型」であると判明!?この宇宙の形状はドーナツ型だった!?
https://news.yahoo.co.jp/expert/articles/dced0aa9ea465861c3f686ae1e435946626692f3
'우주 & 천문학' 카테고리의 다른 글
| 우주의 형태(shape of Universe) (0) | 2024.02.02 |
|---|---|
| NASA, 제임스웹 우주망원경이 포착한 19개의 은하 사진을 공개...적외선 관측으로 드러난 나선은하의 구조 (0) | 2024.02.01 |
| 우주의 크기와 모양 (0) | 2024.01.31 |
| 달이 냉각수축하면서 발생하는 '월진'이 아르테미스 계획이나 월면 콜로니 건설에 악영향을 미칠 가능성 (0) | 2024.01.31 |
| 우주의 형태(곡률) (0) | 2024.01.30 |
| 최근 발견된 초거대 구조 '라니아케아 초은하단'이란 무엇인가 (0) | 2024.01.28 |
| 하루는 조금씩 길어지고 있다...지구의 변화와 공전속도 (0) | 2024.01.24 |
| M87과 처녀자리 은하단 (0) | 2024.01.23 |



