
소수는 '1보다 큰 정수 1과 자기 자신으로만 나누어지는 수로, 영어로는 Prime Number입니다.
※ 여기서 말하는 나누기란 자연수로 나누었을 때 나머지가 0인 경우를 의미합니다.
'1'은 '1보다 큰 정수'가 아니므로 소수가 아닙니다.
'2'는 '1보다 큰 정수'이고 '1과 2 이외의 자연수로 나눌 수 없으므로 소수입니다.
'4'는 '1보다 큰 정수'이지만 '1과 4 이외에도 2로 나누는 것이 가능하므로 소수가 아닙니다.
'5'는 '1보다 큰 정수'이고 1과 5 이외의 자연수로 나눌 수 없으므로 소수입니다.
소수의 정의와 활용법
◆ 소수의 정의
'양의 약수가 1과 자신뿐인 2개로 구성된 자연수'입니다.
참고로, '1'은 소수가 아닙니다.
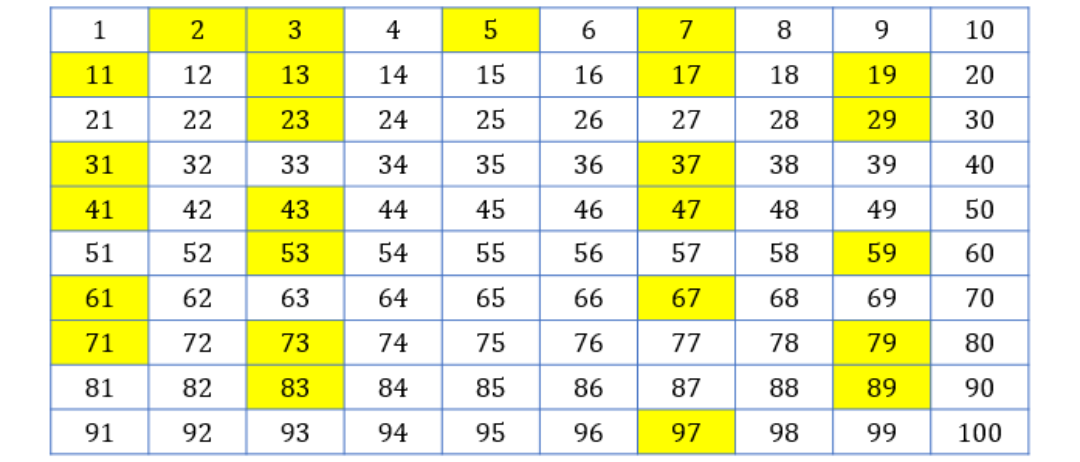
'2'이외의 짝수는 '1과 2와 그 수 자신'이라는 3개 이상의 양의 약수가 있으므로 소수가 아닙니다.
'5' 이외의 1의 자리가 5인 수(15, 25, 35 ...)도 1과 5, 그 수 자신'이라는 3개 이상의 양의 약수가 있으므로 소수가 아닙니다.
이상 10 이상의 숫자에 대해서는 '1의 자리가 1 또는 3, 7, 9인 숫자'에 소수가 있다는 것까지는 규명되었는데, 그 이상의 규칙성은 미궁인 상태입니다.
실제로 소수에서 나타나는 규칙성에 수많은 수학자가 규명을 위해 도전했음에도 불구하고 달성되지 않은 '수학 사상 최대의 난문'이라고 불리고 있습니다.

소인수분해 및 암호
사실 소수의 성질은 다양한 형태로 우리의 일상생활과 밀접하게 관련되어 있습니다. 대표적인 것이 '정보의 암호화'입니다.
예를 들어, '1121893841'이라는 숫자. 이 숫자는 실은 '두 소수 p와 q를 곱셈한 값'인데, p와 q가 무엇인지 알 수 없습니다. 정답은 21193×52937입니다. 답을 알면 정답을 구하는 것이 간단하지만, 답을 모르는 사람은 '1121893841'이라는 숫자에서 두 소수를 도출해내기는 매우 어렵습니다.
이 예에서 사용한 숫자는 10자리이므로 컴퓨터라면 어떻게든 가능하지만, 자릿수가 어느 정도 수준까지 늘어나 버리면 컴퓨터조차 감당해낼 수 없습니다.

이것은 '큰 두 소수의 곱'의 소인수분해에는 효율적으로 답을 찾는 방법이 없다는 것이 원인입니다.
같은 10자리라도 '1000000000'라면, '2로 나누어 5로 나누기를 각 9회 실시함으로써 2^9 × 5^9라고 쉽게 확인할 수 있지만, '1121893841'은 2로도 3으로도 5, 7로도 나누어지지 않아 이를 꾸준히 반복할 수밖에 없고, 이로 인해 터무니없는 계산량이 되어 버립니다.
실제로 2010년 1월 'RSA-768'라는 232자리의 숫자는 소인수분해로 두 소수를 도출하는데 '고성능 컴퓨터 80대'를 동원하여 반년이 걸렸다고 합니다.
No matter how you pursue digital transformation, RSA can help you manage the risk.
https://www.rsa.com/en-us
RSA Cybersecurity and Digital Risk Management Solutions
See why RSA is the market leader for cybersecurity and digital risk management solutions – get research and best practices for managing digital risk.
www.rsa.com
'열쇠가 있으면 간단히 풀 수 있지만, 자물쇠를 아무리 조사해도 알아내기 어렵다'는 이 '열쇠에 필요한 조건'을 고도로 만족시키는 것이 거대한 소수의 곱셈입니다.

당신의 소중한 정보를 보호하는 '소수'의 강점
이 성질을 이용한 것이 'RSA 암호'라는 공개키 암호화입니다.
신용카드나 은행계좌 등 중요한 개인정보 및 금융정보를 관리하는 금융산업에서 정보통신을 안전하게 이루어지도록 하는 중요한 존재가 되었습니다.
'거대한 두 소수의 곱'의 소인수분해 난이도는 자릿수가 증가할 때마다 천문학적인 비율로 높아져 갑니다. 따라서 미래에 컴퓨터가 압도적인 진화를 이루어도 RSA 암호에 사용하는 자릿수를 늘려버리면 보안상 문제가 없다고 알려져 있습니다.
※ 소인수분해를 효율적으로 하는 방법이 발견된다면 암호화 시스템의 변경이 필요하게 될지도 모릅니다.

다만, 이를 확대해석하여 '리만 가설이 증명되면 RSA 암호가 위험에 처한다'라는 이야기도 있습니다만, 리만 가설은 소인수분해의 효율과 관련이 없습니다.
출처 참조 번역
· Wikipedia
'과학 & 기술' 카테고리의 다른 글
| 수백 년 동안 사람들을 공포에 떨게 한 정상의 거인 'Dark Watchers'의 정체 (0) | 2021.03.18 |
|---|---|
| 케첩이 용기의 바닥에 남는 이유는 '비뉴턴 유체'가 되도록 설계되어 있기 때문 (1) | 2021.03.16 |
| 현명한 거인이 찾아낸 소수 '타이타닉 소수' (0) | 2021.03.14 |
| 불가사의한 소수...'수의 원자' (0) | 2021.03.13 |
| 만약 지구 전체가 황금으로 변한다면 무슨 일이 일어날까? (0) | 2021.03.11 |
| 풍력발전의 프로펠러가 거대한 이유 (0) | 2021.03.07 |
| 세계 최초로 '시간결정'의 생성에 성공 (0) | 2021.03.03 |
| 300년 전 특별한 방법으로 봉인된 편지를 X선 스캐너로 가상열람하는 데 성공 (0) | 2021.03.03 |



