
'몬티 홀 문제(Monty Hall problem)'는 결과에 대해 설명을 들어도 납득하기 어려운 것으로 알려진 확률문제인데, 이에 엔지니어 미카엘 파슈키에비치 씨가 실제로 체감할 수 있는 데모를 공개했습니다.
Monty Hall explained
https://www.michalpaszkiewicz.co.uk/blog/montyhallexplained/index.html
몬티 홀 문제는 수학이 상식과 일치하지 않는 것처럼 보이는 좋은 예로, 1975년 스티브 셀빈이 미국 통계학자에게 보낸 편지에서 제시한 것이 처음입니다. 이 문제를 미국의 TV 프로그램 'Let's Make a Deal'이 다루면서 사회자인 몬티 홀의 이름을 따 몬티 홀 문제라고 불리게 되었습니다.

몬티 홀 문제가 다음과 같습니다.

A・B・C라는 라벨이 붙은 3개의 상자가 자리에 준비되어 있고 문제에 도전하는 사람은 이 중에서 하나를 선택합니다. 덧붙여 3개의 상자 중 하나는 당첨이고 나머지 2개는 당첨실패입니다. 어떤 상자가 당첨인지 알고 있는 출제자는 결과를 공개합니다.

다음 도전자는 나머지 상자 중에서 선택합니다. 이때 도전자는 먼저 선택한 상자를 선택해도 좋고 다른 상자로 바꾸어도 되고 이 과정이 반복됩니다.

이 문제의 특이한 점은 먼저 선택한 상자에서 다른 상자로 바꾸는 행위로 인해 당첨확률이 늘어난다는 점입니다. 대부분의 사람은 최종적으로 두 개의 상자에서 당첨이 들어있는 상자를 선택하기 때문에 당첨확률은 1/2(50%)라고 생각합니다. 하지만 먼저 상자를 선택하고 결과가 공개된 후 다른 상자로 바꾸면 당첨확률이 66.6%로 상승하는 것으로 나타났습니다.
3개의 상자 중에서 당첨이 들어있는 확률은 1/3(33.3%)이기 때문에 나머지 상자에 당첨이 들어있는 확률은 2/3(66.6%)입니다. 그러므로 결과를 출제자가 공개하기 전의 시점에서 최초로 선택한 상자 이외를 선택하는 것이 당첨이 나올 확률이 높다고 판단할 수 있습니다.
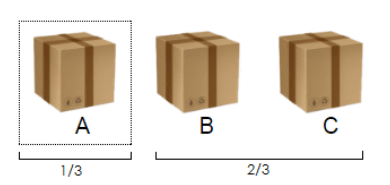
사실 출제자가 당첨이 아닌 상자를 하나 공개해도 아무런 영향도 없습니다. 왜냐하면 최초로 선택한 상자의 당첨확률은 최초와 같은 1/3(33.3%)이기 때문입니다.
파슈키에비치 씨는 몬티 홀 문제를 체험할 수 있는 게임을 공개했는데 웹페이지 아래쪽에 있는 카드로 플레이 할 수 있습니다.
Monty Hall explained
https://www.michalpaszkiewicz.co.uk/blog/montyhallexplained/index.html
Monty Hall explained
How to explain the Monty Hall problem to a disbeliever The Monty Hall problem is an excellent example of a problem where mathematics seem to disagree with common sense. It was first presented as a probability puzzle in a letter by Steve Selvin to the Ameri
www.michalpaszkiewicz.co.uk
더욱 알기 쉬운 예는 카드의 매수를 20장(당첨 1장, 당첨실패 19장)으로 늘려 같은 규칙으로 게임을 플레이한 경우입니다. 이 경우 출제자는 18장의 당첨실패를 공개합니다. 그러면 먼저 선택한 카드의 당첨확률은 1/20(5%)이고 그 이외에 당첨이 포함될 확률은 19/20(95%)입니다. 그 때문에 최초로 선택한 카드와는 다른 카드를 선택한 경우에 당첨을 선택할 확률은 19/20(95%)가 되어 압도적으로 당첨확률이 높아집니다.
'경제' 카테고리의 다른 글
| 국방 명목으로 쓰레기통 1개에 5300만 원의 세금이 지출 (0) | 2023.06.28 |
|---|---|
| 석유산출국이 빠지기 쉬운 부패·내분·빈부격차로부터 노르웨이가 자유로운 이유 (0) | 2023.05.01 |
| 충실한 근로자는 관리직에 의해 공짜로 일하기 쉽다는 연구결과 (0) | 2023.04.30 |
| 2억 1000만 원 상당의 금광석을 호주 아마추어 채굴자가 저렴한 금속탐지기를 사용하여 발견 (0) | 2023.04.05 |
| 다크웹 사이트 'BidenCash'가 216만 건의 신용카드 정보를 1주년 기념으로 무료방출 (0) | 2023.03.06 |
| 일론 머스크의 업무량이 일주일에 120시간 이상에 달해 수면 부족과 등의 통증에 시달리고 있다 (0) | 2023.02.07 |
| 초부유층이 생기는 이유와 세금의 필요성을 이해할 수 있는 웹페이지 (0) | 2022.12.24 |
| 애플이 '스토리'를 무기로 경쟁사를 걷어차며 광고사업을 늘린 성공적인 전략이란? (0) | 2022.08.23 |



